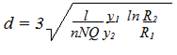Циклон ЛИОЭТ. Высокая степень очистки получается в циклонах системы ЛИОЭТ (Ленинградский институт организации и экономики труда). После входа в циклон благодаря поверхности верхней крышки при первом же своем повороте воздушный поток получает винтовое движение, которое и сохраняется вплоть до выхода воздуха в выхлопную трубу. При поступательно-вращательном движении пыль, находящаяся в воздухе, под действием центробежной силы движется к наружной стенке циклона и, ударяясь об нее, оседает вниз. Наиболее мелкие частицы, не успевшие дойти до наружной стенки циклона, уносятся из циклона через внутреннюю выхлопную трубу.
Для расчета основных размеров циклона принимаются следующие допущения:
1) частицы пыли имеют форму шара;
2) траектория движения шаров принимается плоской;
3) центробежная сила направлена по радиусу циклона (в действительности она направлена нормально к спиралеобразной траектории частицы);
4) отделение пыли происходит после удара ее о наружную стенку циклона.
Сопротивление воздуха движущемуся в нем телу выражается величиной
S=kF v2 y1= kF v2 p1 (1)
2g 2
где k — коэффициент сопротивления;
F — площадь миделевого сечения, т. е. наибольшая площадь сечения тела, перпендикулярного направлению его движения;
v — скорость движения частицы;
y — удельный вес воздуха;
р1 — плотность воздуха.
Величина центробежной силы, развивающейся при вращении частицы, равна
C = mw2 (2)
x
где т —- масса частицы;
w — скорость вращения частицы;
х — расстояние ее от центра циклона.
При этом
w=Qx (3)
где Q — угловая скорость вращения частицы.
Поэтому
C = m Q2x2 = mQ2x,
x
масса частицы равна
m= пd3 p2
6
где р2 — ее плотность.
При равномерном движении частицы от внутреннего цилиндра к наружному существует равновесие между центробежной силой и сопротивлением воздуха движущейся частицы (шара) или
С = пd3 p2 Q2 x = k пd2 * v2 p1 (4)
6 4 2
Откуда
4 dQ2xp2 = kp1v2 (5)
3
Коэффициент сопротивления k есть функция числа Рейнольдса
Re= vd
l
где v — скорость пылинки в м/сек; d — диаметр пылинки в м; l —кинематическая вязкость воздуха в м2/сек.
Для всех случаев, когда при движении пылинки Re <= l, сопротивление воздуха движущемуся в нем шару изменяется по закону Стокса. В этом промежутке значений, когда Re <= l, коэффициент сопротивления выражается величиной
k = 24 (6)
Re
или
k = 24
vd
Подставляя значение k в формулу (1) получим
S= 24l nd2 v2 p1= 3nvdp1l
dv 4 2
Отсюда видно, что при Re <= l сопротивление движению пылинки пропорционально скорости в первой степени и обтекание пылинки потоком соответствует ламинарному режиму.
Если l < Re< 103, то коэффициент сопротивления выражается величиной
В этом случае
S = 3nvdp1 l1 + 4l 1/3 * nd 2 * v2 _p1
v 1/3 d 1/3 4 2
или
S = 3nvdp1 l+1 nd 5/3 v 5/3 p1l 1/3 (8)
2
Таким образом, мы видим, что с увеличением числа Re, т. е. с увеличением скорости, сопротивление воздушной среды начинает зависеть от скорости v 5/3, т. е. постепенно приближается к квадратичной зависимости.
В пределах1*103 < Re < 2,5*105 наблюдается квадратичная зависимость сопротивления от скорости и обтекание пылинки соответствует турбулентному режиму.
Движение пылинки в пространстве между внутренним и наружным цилиндрами циклона вообще происходит при малых числах Re, однако, не зная размеров циклона, нельзя заранее определить и число Re; по этому при расчете циклона сначала следует задаться характером обтекания пылинок, рассчитать циклон, а затем проверить.
Допустим предварительно, что Re <= 1, тогда, подставляя в формулу(5) значение k из формулы (6)
4 dQ2xp2 = 24l p1v2 = 24l vp1
3 vd d
Откуда
v = dx = d2Q2p2 x
dt 1 8lp1
или
dt = 18lp1 dx
d2Q2p2 x
Интегрируя в пределах переменного от R1 до R2 получим
t = 18lp1 ln R2
d2Q2p2 R1
Отношение плотностей можно заменить отношением объемных весов воздуха y1 /y2, тогда получим
t = 18l y1 ln R2(9)
d2Q2y2 R1
При расчете циклонов сначала принимают скорость в выхлопном отверстии циклона и по расходу пыльного воздуха определяют R1, а затем, сообразуясь с размером нагнетательной трубы, подходящей тангенциально к циклону, определяют R2.
Далее, принимая минимальный диаметр частицы осаждаемой пыли равным d и зная объёмные веса y1 иy2 из уравнения (9), определяют время прохождения в циклоне самой невыгодно расположенной частицы пыли, т.е. той частицы, которая в момент поступления пыльного воздуха в циклоне находилась вблизи его внутренней стенки; затем вычисляется путь частицы, число витков воздуха в циклоне и высота цилиндрической части циклона.
Если w-средняя окружная скорость воздушного потока в циклоне, то путь воздушного потока будет wt
Средний радиус циклона R0
R0 = R1 + R2
2
При числе оборотов воздушного потока в циклоне, равным N, тот же путь потока будет
2n R0N= wt
Откуда
t=2nR0N = 2nN (10)
w Q
Подставляем это значение t в уравнение (9)
2nN =18l y1 ln R2
Q d2Q2y2 R1
Откуда получим значение минимальных диаметров пылинок, осаждаемых в циклоне
Пусть имеется циклон с наружным радиусом R2. Считая в формуле (11) величину R2 постоянной и R1 переменной, а также что движущиеся частицы находятся на расстоянии R1, получим переменные величины минимальных диаметров пылинок, осаждаемых в циклоне. Минимальный диаметр будет у частиц, непосредственно прилегающих к наружной стенке циклона, в том случае, когда R1= R2 (d=0). По мере уменьшения величины диаметр осаждающихся частиц увеличивается. Следовательно, у наружной стенки циклона степень очистки составляет 100%; ближе к внутренней стенке степень очистки уменьшается.